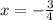The graphs intersect at two points:
x = 1
x = -3/4
Let's find all the points of intersection between the graphs of the functions a(x)=(x+4)(x-1) and b(x)=(-3x+1)(x-1).
We can find these points by solving the system of equations formed by setting the two functions equal to each other:
a(x)=b(x)
Steps to solve:
1. Distribute both sides:
(x+4)(x−1)=(−3x+1)(x−1)
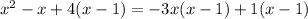
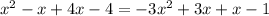
2. Combine like terms:
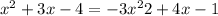
3. Move terms to one side and combine like terms:
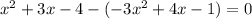
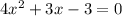
4. Solve the quadratic equation:
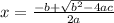
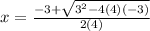
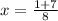
5. Separate the solutions:
x=1