Question

I uploaded an image of the problem :)

Answer 1

Initial size of the culture = 128

Doubling period = 7.56 minutes (2 d.p.)

Population after 80 minutes = 195,313 (nearest integer)

Population will reach 15,000 = 51.99 minutes (2 d.p.)

Explanation:

The general form of an exponential function is:

`\boxed{\begin{array}{l}\underline{\textsf{General form of an Exponential Function}}\\\\\large\text{$y=ab^x$}\\\\\textsf{where:}\\\phantom{ww}\bullet\;\textsf{$a$ is the initial value ($y$-intercept).}\\ \phantom{ww}\bullet\;\textsf{$b$ is the base (growth/decay factor) in decimal form.}\end{array}}`

In this case:

• Let x be the time (in minutes).
• Let y be the count of bacteria.

Given that the count in a bacteria culture was 800 after 20 minutes and 2000 after 30 minutes, we can substitute these values into the exponential function formula and set up the following two equations:

`ab^(20)=800`

`ab^(30)=2000`

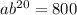
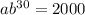
To find the base (b), divide the equations to eliminate a:

`(ab^(30))/(ab^(20))=(2000)/(800)`

`(b^(30))/(b^(20))=(5)/(2)`

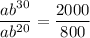
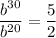
Now, solve for b:

`b^(30-20)=(5)/(2)`

`b^(10)=(5)/(2)`

`b^(10)=\left((5)/(2)\right)^{(1)/(10)}`

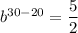
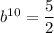
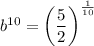
To find the value of a, substitute the exact value of b into one of the equations:

`a\left(\left((5)/(2)\right)^{(1)/(10)}\right)^(20)=800`

`a\left((5)/(2)\right)^2=800`

`a\left((25)/(4)\right)=800`

`a=128`

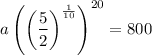
Therefore, the initial size of the culture was 128.

The equation that models the count of the bacteria after x minutes is:

`y=128 \cdot \left((5)/(2)\right)^{(x)/(10)}`

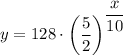
This can be simplified to:

`\large\boxed{\boxed{y=128 \cdot \left(2.5\right)^(0.1x)}}`

To find the doubling period given that the initial size of the culture was 128, set y = 256 and solve for x:

`128 \cdot \left(2.5\right)^(0.1x)=256`

`\left(2.5\right)^(0.1x)=2`

`\ln\left(\left \left(2.5\right)^(0.1x)\right)=\ln(2)`

`0.1x\ln\left(2.5\right)=\ln(2)`

`x=(\ln(2))/(0.1\ln\left(2.5\right))`

`x=7.56470797366...`

`x=7.56\; \sf minutes\;(2\;d.p.)`

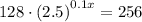
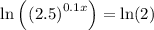
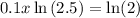
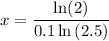
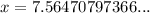
Therefore, the doubling period is 7.56 minutes (rounded to 2 decimal places).

To find the population after 80 minutes, substitute x = 80 into the equation and solve for y:

`y=128 \cdot \left(2.5\right)^(0.1 \cdot 80)`

`y=128 \cdot \left(2.5\right)^(8)`

`y=128 \cdot \left(1525.87890625\right)`

`y=195312.5`

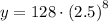
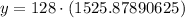
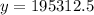
Therefore, the population after 80 minutes is approximately 195,313 (rounded to the nearest integer).

To determine when the population will reach 15,000, substitute y = 15000 into the equation and solve for x:

`128 \cdot \left(2.5\right)^(0.1x)=15000`

`\left(2.5\right)^(0.1x)=117.1875`

`\ln\left(\left(2.5\right)^(0.1x)\right)=\ln\left(117.1875\right)`

`0.1x\ln\left(2.5\right)=\ln\left(117.1875\right)`

`x=(\ln\left(117.1875\right))/(0.1\ln\left(2.5\right))`

`x=51.989778467...`

`x=51.99\; \sf minutes\;(2\;d.p.)`

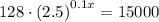
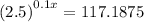
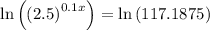
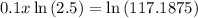
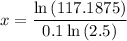
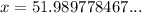
Therefore, the population will reach 15,000 after 51.99 minutes (rounded to two decimal places).