Answer:
radius ≈ 10cm
Explanation:
The volume (
 ) of a cone is given by the formula:
) of a cone is given by the formula:
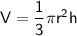
Where:
-
 is the radius of the base,
is the radius of the base,
-
 is the height.
is the height.
In this case, we're given the height (
 ) and the volume (
) and the volume (
 ). we need to find the radius (
). we need to find the radius (
 ).
).
Let's rearrange the formula to solve for the radius (
 ):
):
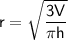
Now, substitute the given values:

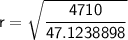
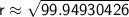
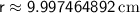
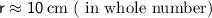
Therefore, the radius of the cone's base is approximately
 .
.