Question

Calculate the length of the space diagonal AG
in the cuboid shown

Answer 1

Exact length = 9√2 cm

Rounded length = 12.7 cm

Explanation:

The space diagonal of a rectangular prism is the diagonal connecting opposite corners. In other words, it is a line that goes from a vertex of the prism, through the center of the prism, to the opposite vertex.

The general formula for the length of a space diagonal is:

`d=√(x^2+y^2+z^2)`

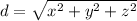
where x, y and z are the width, height and length of the prism.

In this case:

• d = AG
• Width: x = 4 cm
• Height: y = 5 cm
• Length: z = 11 cm

Substitute the values into the formula and solve for AG:

`AG=√(4^2+5^2+11^2)`

`AG=√(16+25+121)`

`AG=√(162)`

`AG=√(9^2 \cdot 2)`

`AG=√(9^2) √( 2)`

`AG=9√(2)\; \sf cm`

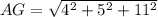
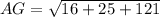
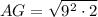
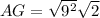
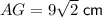
Therefore, the exact length of the space diagonal is 9√2 cm, or approximately 12.7 cm (rounded to the nearest tenth).