Question

Find how much money needs to be deposited now into an account to obtain $5,200 (Future Value) in 14 years if the interest rate is 4.5% per year compounded annually.

The necessary present value (principal deposit) necessary is $

Round your answer to 2 decimal places

Answer 1

$2,807.86

Explanation:

To determine how much money needs to be deposited in an account to obtain a future value of $5,200 in 14 years given the interest rate is 4.5% per year compounding annually, we can use the future value formula:

`\boxed{\begin{array}{l}\underline{\textsf{Future Value Formula}}\\\\FV=P\left(1+(r)/(n)\right)^(nt)\\\\\textsf{where:}\\\phantom{ww}\bullet\;\;\textsf{$FV$ is the future value.}\\\phantom{ww}\bullet\;\;\textsf{$P$ is the principal amount invested.}\\\phantom{ww}\bullet\;\;\textsf{$r$ is the interest rate (in decimal form).}\\\phantom{ww}\bullet\;\;\textsf{$n$ is the number of times interest is applied per year.}\\\phantom{ww}\bullet\;\;\textsf{$t$ is the time (in years).}\end{array}}`

In this case:

• FV = $5,200
• r = 4.5% = 0.045
• n = 1 (compounded annnually)
• t = 14 years

Substitute the values into the formula:

`5200=P\left(1+(0.045)/(1)\right)^(14 \cdot 1)`

Solve for P:

`5200=P\left(1+0.045\right)^(14)`

`5200=P\left(1.045\right)^(14)`

`P=(5200)/((1.045)^(14))`

`P=(5200)/(1.8519449216...)`

`P=2807.8588835...`

`P=2807.86`

Therefore, the amount of money that needs to be deposited now is $2,807.86, rounded to two decimal places.

Answer 2

$2807.86

Explanation:

In order to find the present value we can use future value formula:

The future value (FV) formula for compound interest is given by:

`\sf FV = PV * (1 + r)^t`

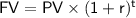
Where:

-
`\sf FV` is the future value (in this case, $5,200),

-
`\sf PV` is the present value or principal deposit (what we want to find),

-
`\sf r` is the annual interest rate (4.5% or 0.045 in decimal form), and

-
`\sf t` is the number of years (14).

We want to rearrange this formula to solve for the present value (
`\sf PV`):

`\sf PV = (FV)/((1 + r)^t)`

Now, plug in the values:

`\sf PV = (5200)/((1 + 0.045)^(14))`

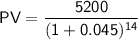
Calculate this expression to find the necessary present value:

`\sf PV = (5200)/((1.045)^(14))`

`\sf PV \approx (5200)/(1.851944922)`

`\sf PV \approx 2807.858884`

`\sf PV \approx 2807.86 \textsf{ (in 2 d.p.)}`

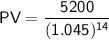
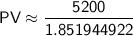
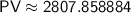
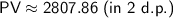
Therefore, the necessary present value (principal deposit) to obtain $5,200 in 14 years with an annual interest rate of 4.5% compounded annually is approximately $2807.86 (rounded to 2 decimal places).