Question

Which statement is true about their work? Neither student solved for k correctly because K = 2 and StartFraction 1 over 8 EndFraction. Only Adler solved for k correctly because the inverse of addition is subtraction. Only Erika solved for k correctly because the opposite of One-half is Negative one-half. Both Adler and Erika solved for k correctly because either the addition property of equality or the subtraction property of equality can be used to solve for k.

Answer 1

Answer: Both Adler and Erika are correct

Explanation:

On Edge 2021

Answer 2

Question:

Adler and Erika solved the same equation using the calculations below.

Adler’s Work

`(13)/(8)= k + (1)/(2)`

`(13)/(8) - (1)/(2) = k + (1)/(2) -(1)/(2)`

`(9)/(8)= k`

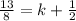
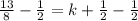
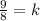
Erika’s Work

`(13)/(8)= k + (1)/(2)`

`(13)/(8)+ (-(1)/(2)) = k + (1)/(2) + (-(1)/(2)).`

`(9)/(8)= k`

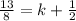
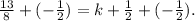
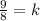
Which statement is true about their work?

Answer:

Both Adler and Erika solved for k correctly because either the addition property of equality or the subtraction property of equality can be used to solve for k.

Explanation:

Given

`(13)/(8)= k + (1)/(2)`

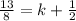
Required

What is true about Adler and Erika's workings

Analyzing Adler's work;

`(13)/(8)= k + (1)/(2)`

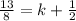
Adler subtracted 1/2 from both sides

`(13)/(8) - (1)/(2) = k + (1)/(2) -(1)/(2)`

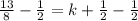
Solving the expression on the left-hand side

`(13)/(8) - (1)/(2) = (13 - 4)/(8) = (9)/(8)`

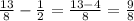
Solving the expression on the right-hand side

`k + (1)/(2) - (1)/(2) = k`

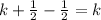
Hence:

`(9)/(8)= k`

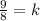
So, Adler's workings is correct

Analyzing Erika's work;

`(13)/(8)= k + (1)/(2)`

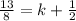
Erika added -1/2 to both sides

`(13)/(8)+ (-(1)/(2)) = k + (1)/(2) + (-(1)/(2)).`

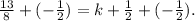
Solving the expression on the left-hand side

`(13)/(8) + (-(1)/(2)) = (13)/(8) - (1)/(2) = (13 - 4)/(8) = (9)/(8)`

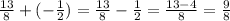
Solving the expression on the right-hand side

`k + (1)/(2) + (-(1)/(2)) =k + (1)/(2) - (1)/(2) = k`

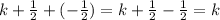
Hence:

`(9)/(8)= k`

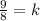
So, Erika's workings is correct

Both workings are correct