Question

Find the values of x, y, and z. Round to the nearest tenth, if necessary.

(choices are 3.6, 4.5, and 6.5)

Answer 1

Answer: x= 4.5, y=3.6, z=6.5

Explanation:

To find : x, y and z.

First label the triangle as A,B,C and D (as in the picture below).

ΔABC , ΔACD and ΔABD both are right triangles.

In ΔABC ,

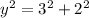`y^2=3^2+2^2` [By Pythagoras theorem]

`\Rightarrow\ y^2=13\\\\\Rightarrow\ y=√(13)\approx3.6`

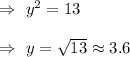
In ΔACD ,

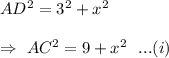`AD^2=3^2+x^2\\\\\Rightarrow\ AC^2=9+x^2 \ \ ...(i)` [By Pythagoras theorem]

In ΔABC ,

`y^2+AC^2=(2+x)^2\\\\\Rightarrow\ AC^2=(2+x)^2-y^2\ \ ...(ii)`

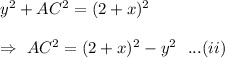
From (i) and (ii), we get

`9+x^2=(2+x)^2-y^2\\\\\Rightarrow\ 9+x^2=4+x^2+4x-(3.6)^2\\\\\Rightarrow\ 9=4+4x-12.96\\\\\Rightarrow\ 4x=9-4+12.96\\\\\Rightarrow 4x= 17.96\\\\\Rightarrow\ x=(17.96)/(4)\\\\\Rightarrow\ x=4.49\approx4.5`

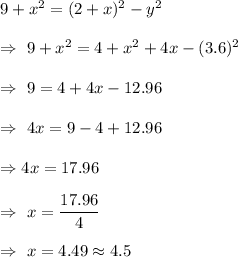
Z = 2+x= 2+4.5 =6.5

Hence, x= 4.5, y=3.6, z=6.5