Answer:
1.
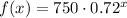
Explanation:
The cell phone experiments an exponential depreciation, which is defined by the following formula:
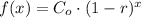 , for
, for
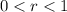 . (1)
. (1)
Where:
 - Initial cost, measured in monetary units.
- Initial cost, measured in monetary units.
 - Depreciation rate, no unit.
- Depreciation rate, no unit.
 - Time, measured in years.
- Time, measured in years.
 - Current value of the cell phone, measured in monetary units.
- Current value of the cell phone, measured in monetary units.
If we know that
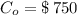 and
and
 , then the exponential decay function that represents the situation is:
, then the exponential decay function that represents the situation is:
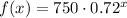
Which means that correct answer is 1.