Answer:
c) C

Explanation:
Explanation:-
Normal distribution
A random variable 'x' is said to have a normal distribution. if its identity function or probability is given by
f( x,μ,σ) =
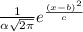 ...(i)
...(i)
Here 'b' be the mean of the normal distribution
And σ be the standard deviation
and C = 2σ²
Now, the equation (i) changes to
 this represents the normal graph
this represents the normal graph
where A =
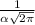 and C = 2σ²
and C = 2σ²