1 Answer

Corey Waldon · Answer 1 · 2022-01-28T02:08:37+0000

Given:

PQRS is a circle, PQT and SRT are straight lines.

To find:

The value of x.

Solution:

Since PQRS is a circle, PQT and SRT are straight lines, therefore, PQRS isa cyclic quadrilateral.

We know that, sum of opposite angles of a cyclic quadrilateral is 180 degrees.

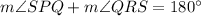
$m\angle SPQ+m\angle QRS=180^\circ$

$81^\circ+m\angle QRS=180^\circ$

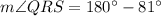
$m\angle QRS=180^\circ-81^\circ$

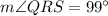
$m\angle QRS=99^\circ$

Now, SRT is a straight line.

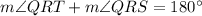$m\angle QRT+m\angle QRS=180^\circ$ (Linear pair)

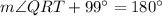
$m\angle QRT+99^\circ=180^\circ$

$m\angle QRT=180^\circ-99^\circ$

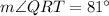$m\angle QRT=81^\circ$ ...(i)

According to the Exterior angle theorem, in a triangle the measure of an exterior angle is equal the sum of the opposite interior angles.

Using exterior angle theorem in triangle QRT, we get

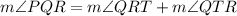
$m\angle PQR=m\angle QRT+m\angle QTR$

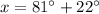
$x=81^\circ+22^\circ$

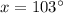
$x=103^\circ$

Therefore, the value of x is 103 degrees.

Please log in or register to add a comment.