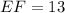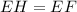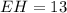Question

C. Line m is a perpendicular
bisector. If EG=12 and FG=5,
of then how long is:

Answer 1

`EF = 13`

`GH = 5`

`EH = 13`

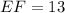
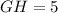
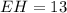
Explanation:

Given

The attached figure

`EG = 12`

`FG = 5`

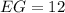
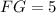
Solving (a): EF

Since m is a perpendicular bisector, then <EGF and <EGH are right-angled.

So, EF will be calculated using Pythagoras theorem which states:

`EF^2 = EG^2 + FG^2`

`EF^2 = 12^2 + 5^2`

`EF^2 = 144 + 25`

`EF^2 = 169`

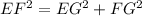
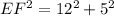
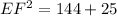
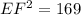
Take the positive square roots of both sides

`EF = \sqrt{169`

`EF = 13`

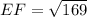
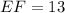
Solving (b): GH

Since m is a perpendicular bisector, then GH = FG

`FG = 5`

`GH = FG`

`GH = 5`

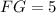
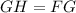
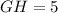
Solving (c): EH

Since m is a perpendicular bisector, then EH = EF

`EF = 13`

`EH = EF`

`EH = 13`