Given

 , and
, and
 in similar triangles
in similar triangles
 and
and
 , using the ratio of corresponding sides,
, using the ratio of corresponding sides,
 equals 7.5 units.
equals 7.5 units.
Sure, let's solve step by step using the properties of similar triangles.
Given:
 ,
,
 ,
,
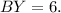
We have two parallel lines
 and
and
 intersected by transversal (AB), which creates similar triangles (BXY) and (BAC).
intersected by transversal (AB), which creates similar triangles (BXY) and (BAC).
The ratio of corresponding sides in similar triangles is equal:
 =
=

Substituting the given values:
 =
=
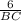
To solve for
 cross multiply:
cross multiply:
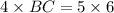
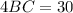
Divide both sides by 4 to isolate
 :
:
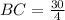
Simplify:
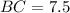
Therefore,
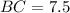 .
.