Question

Does anyone know the answer

Answer 1

The value of sinθ is -√13/4.

To find the value of sinθ, we can use the identity
`sin^2`θ +
`cos^2`θ = 1. Given that cos(-θ) = √3/4 and sinθ < 0, we can solve for sinθ as follows:

1. Recall that cos(-θ) is equal to cosθ. So, we have cosθ = √3/4.

2. Using the identity
`sin^2`θ +
`cos^2`θ = 1, we can substitute the value of cosθ to solve for sinθ. This gives us:

`sin^2`θ +
`(√(3) /4)^2` = 1

`sin^2`θ + 3/16 = 1

`sin^2`θ = 1 - 3/16

`sin^2`θ = 13/16

3. Since sinθ < 0, we know that sinθ is negative.

4. Taking the square root of both sides, we find:

sinθ = -
`√((13/16))`

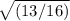
Simplifying further, sinθ = -√13/4.

Therefore, the value of sinθ is -√13/4.