the equation of the exponential function is approximately:
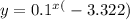
The general form of an exponential function is y = a^bx, where a is the initial value, b is the constant multiplier (often called the base), and x is the independent variable.
To find the equation of the exponential function represented by the table, we can use the given points to solve for a and b.
For example, we can see that when x = 0, y = 0.1. This means that a = 0.1.
We can then use another point, such as (1, 2), to solve for b. Plugging these values into the equation, we get:
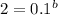
Taking the logarithm of both sides (to base 10), we get:
log(2) = b log(0.1)
b ≈ -3.322
Therefore, the equation of the exponential function is approximately:
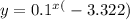
This is just one possible solution, as there are other exponential functions that could also fit the data in the table. However, this is the most common form of an exponential function, and it is a good starting point for further analysis.