Answer: At point (
 )
)
Explanation: Diagonal is a line uniting two opposite points. In a square, the diagonals intersect in a 90° and bisect each other, i.e., divides each diagonal into two segments of the same length.
In other words, the diagonals of a square meet at their midpoint, which is found as the following:
(x,y) =
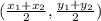
The opposite vertices of the given square are (-2,6) and (1,-7).
So, the intersection is
(x,y) =
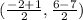
(x,y) =
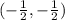
The diagonals of square with vertices (-2,6)(6,1)(1,-7)(-7,-2) intersect at point
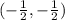 .
.