The solution is
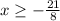 or in interval notation
or in interval notation

To solve the inequality
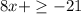 , we'll follow these steps:
, we'll follow these steps:
1. Subtract 8x from both sides:
![\[ 8x + 8x + \geq -21 - 8x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hoeja1l16lqhs5l971sp7414olpoh345bw.png)
This simplifies to:
![\[ 0 \geq -21 - 8x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2y178v7kqslju4sezi9p3fx4lvfcx32xwr.png)
2. Add 21 to both sides to isolate the term with x:
![\[ 0 + 21 \geq -21 - 8x + 21 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zer4278fk8qwresshei1zgi6fqp83g2afh.png)
This simplifies to:
![\[ 21 \geq -8x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pwydfnovey3mj5j9vodbrymxe8cgk1w8c9.png)
3. Divide both sides by -8 (note: since we're dividing by a negative number, the inequality sign flips):
![\[ (21)/(-8) \leq (-8x)/(-8) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/au8ers7vbun0g8i3tx874488l4lgdalyj1.png)
This results in:
![\[ -(21)/(8) \leq x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/v5mjpno4g2l9lo3b5csvoi4ob78f9pcxaw.png)
So, the solution to the inequality is x such that x is greater than or equal to
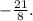 In interval notation, the solution is
In interval notation, the solution is
 This means any value of x within or greater than this interval satisfies the original inequality.
This means any value of x within or greater than this interval satisfies the original inequality.