Question

The Towers of Hanoi Problem is often used

as an example when teaching recursion. Six
disks of different sizes are piled on a peg
in order by size, with the largest at the bottom.
There are two empty pegs. The problem is to move
all the disks to the third peg by moving only
one at a time a never placing a disk on top of
a smaller one. The second intermediate moves. Write
a peg may be used for recurrence equation
Considering n disks to determine the number
of moves done, and solve it to determine the
Complexity of the algorithm.

Answer 1

The Towers of Hanoi problem is a classic example of recursion used to teach problem-solving. The time complexity of the Towers of Hanoi algorithm is exponential, with the number of moves increasing exponentially with the number of disks.

Step-by-step explanation:

The Towers of Hanoi problem is a classic example used to teach recursion. It involves moving a stack of disks from one peg to another, following certain rules. To determine the number of moves required to solve the problem for a given number of disks, we can use a recurrence equation.

The recurrence equation for the Towers of Hanoi problem with n disks can be defined as follows:

1. If n = 0, the number of moves is 0.
2. Otherwise, the number of moves is 2 times the number of moves required for (n-1) disks, plus 1.

Using this recurrence equation, we can solve for the number of moves required for different numbers of disks. The time complexity of the Towers of Hanoi algorithm is exponential, specifically O(2^n), which means the number of moves increases exponentially with the number of disks.

Answer 2

The Towers of Hanoi problem is a classic example used in teaching recursion. The recurrence equation to determine the number of moves done is
`T(n) = 2^n - 1`. The complexity of the algorithm is
`O(2^n)`.

Step-by-step explanation:

The Towers of Hanoi problem is a classic example used to teach recursion. It involves moving a pile of disks from one peg to another, following certain rules. Let's illustrate the steps and explain the procedure in pseudocode:

1. The problem begins with all the disks on the starting peg, labeled as "source," and two empty pegs, labeled as "spare" and "destination."

2. To solve the problem recursively, we can break it down into smaller subproblems. We'll define a recursive function, let's call it "moveDisks," that takes the following parameters:

• - The number of disks to move, denoted as "n"
• - The source peg, denoted as "source"
• - The destination peg, denoted as "destination"
• - The spare peg, denoted as "spare"

3. The base case for the recursion is when there is only one disk to move. In this case, we can simply move the disk from the source peg to the destination peg.

4. For the recursive case, we'll follow these steps:

a. Call the "moveDisks" function recursively with parameters:

• - n-1 as the number of disks to move
• - source as the source peg
• - spare as the destination peg
• - destination as the spare peg

This step moves all but the last disk from the source peg to the spare peg.

b. Move the last disk from the source peg to the destination peg.

c. Call the "moveDisks" function recursively with parameters:

• - n-1 as the number of disks to move
• - spare as the source peg
• - destination as the destination peg
• - source as the spare peg

This step moves all the disks from the spare peg to the destination peg.

5. Here is the pseudocode for the "moveDisks" function:

function moveDisks(n, source, destination, spare):

if n == 1:

move disk from source to destination

else:

moveDisks(n-1, source, spare, destination)

move disk from source to destination

moveDisks(n-1, spare, destination, source)

Next, let's determine the recurrence equation for the number of moves done and solve it to determine the complexity of the algorithm.

The recurrence equation for the number of moves, denoted as "T(n)," can be defined as follows:

`T(n) = 2 * T(n-1) + 1`

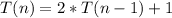
The base case is
`T(1) = 1`, as it takes one move to move a single disk.

Solving this recurrence equation, we can find that the complexity of the algorithm is
`O(2^n)` because for each additional disk, the number of moves approximately doubles. This exponential growth is the characteristic of the Towers of Hanoi problem.