Final answer:
The Towers of Hanoi problem is a classic example used in teaching recursion. The recurrence equation to determine the number of moves done is
 . The complexity of the algorithm is
. The complexity of the algorithm is
 .
.
Step-by-step explanation:
The Towers of Hanoi problem is a classic example used to teach recursion. It involves moving a pile of disks from one peg to another, following certain rules. Let's illustrate the steps and explain the procedure in pseudocode:
1. The problem begins with all the disks on the starting peg, labeled as "source," and two empty pegs, labeled as "spare" and "destination."
2. To solve the problem recursively, we can break it down into smaller subproblems. We'll define a recursive function, let's call it "moveDisks," that takes the following parameters:
- - The number of disks to move, denoted as "n"
- - The source peg, denoted as "source"
- - The destination peg, denoted as "destination"
- - The spare peg, denoted as "spare"
3. The base case for the recursion is when there is only one disk to move. In this case, we can simply move the disk from the source peg to the destination peg.
4. For the recursive case, we'll follow these steps:
a. Call the "moveDisks" function recursively with parameters:
- - n-1 as the number of disks to move
- - source as the source peg
- - spare as the destination peg
- - destination as the spare peg
This step moves all but the last disk from the source peg to the spare peg.
b. Move the last disk from the source peg to the destination peg.
c. Call the "moveDisks" function recursively with parameters:
- - n-1 as the number of disks to move
- - spare as the source peg
- - destination as the destination peg
- - source as the spare peg
This step moves all the disks from the spare peg to the destination peg.
5. Here is the pseudocode for the "moveDisks" function:
function moveDisks(n, source, destination, spare):
if n == 1:
move disk from source to destination
else:
moveDisks(n-1, source, spare, destination)
move disk from source to destination
moveDisks(n-1, spare, destination, source)
Next, let's determine the recurrence equation for the number of moves done and solve it to determine the complexity of the algorithm.
The recurrence equation for the number of moves, denoted as "T(n)," can be defined as follows:
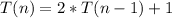
The base case is
 , as it takes one move to move a single disk.
, as it takes one move to move a single disk.
Solving this recurrence equation, we can find that the complexity of the algorithm is
 because for each additional disk, the number of moves approximately doubles. This exponential growth is the characteristic of the Towers of Hanoi problem.
because for each additional disk, the number of moves approximately doubles. This exponential growth is the characteristic of the Towers of Hanoi problem.