Question

Prove the Identity

rule options are:
- Algebra
- Reciprocal
- Quotient
- Pythagorean
- Odd/Even
- Evaluation
- Sum and Difference

Answer 1

To prove the identity
`\((\sin(\pi - x))/(\sin(x + (\pi)/(2))) = \tan x\)`, let's follow a step-by-step proof using the given rules

Identity to be Proven:

`\[ (\sin(\pi - x))/(\sin(x + (\pi)/(2))) = \tan x \]`

Proof:

Step 1: We apply the Sum and Difference identity for sine:

`\(\sin(\pi - x) = \sin \pi \cos x - \cos \pi \sin x\).`

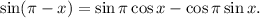
- Rule Used: Sum and Difference

`\[ (\sin(\pi - x))/(\sin(x + (\pi)/(2))) = (\sin \pi \cos x - \cos \pi \sin x)/(\sin(x + (\pi)/(2))) \]`

Step 2: We simplify the expression using the trigonometric values for
`\(\sin \pi\)` and
`\(\cos \pi\)`:

- Rule Used: Evaluation

`\[ (\sin(\pi - x))/(\sin(x + (\pi)/(2))) = (0 \cdot \cos x - (-1) \cdot \sin x)/(\sin(x + (\pi)/(2))) \]`

`\[ = (\sin x)/(\sin(x + (\pi)/(2))) \]`

Step 3: We apply the Sum and Difference identity for sine:

`\(\sin(x + (\pi)/(2)) = \cos x\).`

- Rule Used: Sum and Difference

`\[ (\sin(\pi - x))/(\sin(x + (\pi)/(2))) = (\sin x)/(\cos x) \]`

Step 4: We use the Quotient identity for tangent:

`\(\tan x = (\sin x)/(\cos x)\).`

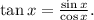
- Rule Used: Quotient

`\[ (\sin(\pi - x))/(\sin(x + (\pi)/(2))) = \tan x \]`

The proof is complete, and the given identity has been verified using the provided rules.