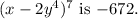The coefficient of
 in the expansion of
in the expansion of
 is -672, obtained by applying the binomial theorem with k = 5 and evaluating the expression step by step.
is -672, obtained by applying the binomial theorem with k = 5 and evaluating the expression step by step.
Let's break down the calculation step by step.
The general term in the expansion of
 is given by the binomial theorem:
is given by the binomial theorem:
![\[T_k = \binom{7}{k} x^(7-k) (-2y^4)^k\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yrmscejh9dev7e3rc2wbwxcgc1ehew9y4q.png)
Now, for the term corresponding to
 , we need to find the value of \(k\) that satisfies two conditions:
, we need to find the value of \(k\) that satisfies two conditions:
1. The power of x: 7 - k = 2 (because we want
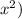
2. The power of y: 4k = 20 (because we want
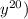
Solving 7 - k = 2 gives k = 5. Substituting this into 4k = 20 confirms that it's satisfied.
Now, plug k = 5 into the general term formula:
![\[T_5 = \binom{7}{5} x^(7-5) (-2y^4)^5\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/hnk78l5byh9ofzhos0h6iur702c74fs0vh.png)
Simplify this expression:
![\[T_5 = \binom{7}{5} x^2 (-32y^(20))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/66ex9su27ape4lz5iehoisjcb1dh10ytf4.png)
Now, calculate the binomial coefficient:
![\[\binom{7}{5} = (7!)/(5!(7-5)!) = (7 * 6)/(2) = 21\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/3hu99k6jyftwcyhugfd274lpe42umjn1z3.png)
Substitute this back into the expression:
![\[T_5 = 21 * x^2 * (-32y^(20))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1h6vtdq0bcgawa0gzjpguujpu8rbz1g2hb.png)
Finally, calculate the coefficient:
![\[21 * (-32) = -672\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/6xadt3c3yd3ncnin4u1jerhx6kfalbfc04.png)
So, the coefficient of
 in the expansion of
in the expansion of