Answer:
32
Explanation:
You have to use pythagorean theorem for this, where a and b represent the 2 sides while c represents the hypoteneuse.
a²+b²=c²
If the diagonal of a square is 8, it divides the square into 2 triangles, both with a hypoteneuse of 8. Since it is a square, that means the other 2 sides will have equal lengths. So input 8 into the equation:
a²+b²=8²
a²+b²=64
Then you can change a and b into the same variable, since you know they will be equal due to you working with a square.
a²+a²=64
simplify: 2a²=64
divide both sides by 2: a²= 32
square root both sides: a =

then you know the length of each side is

to find the area of a square, you must multiply both sides by each other, so do
 *
*
 , which will give you 32 since you are essentially doing this:
, which will give you 32 since you are essentially doing this:
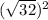 in which the square and square root cancel out.
in which the square and square root cancel out.