Question

Which of the following quadratic polynomials has zeroes at 3/5 - 3/5ᵢ and 3/5 + √3/5 ?

A) x² - 6/5x + 24/25
B) x² - 6/5x + 27/25
C) x² - 3/5x + 24/25
D) x² - 3/5x + 27/25

Answer 1

The quadratic polynomial with zeroes at
`\( (3)/(5) - (3)/(5)i \) and \( (3)/(5) + (√(3))/(5) \) is \( \mathbf{\text{Option D: } x^2 - (3)/(5)x + (27)/(25)} \).`

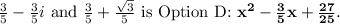
Step-by-step explanation:

To find the quadratic polynomial with the given zeroes, we can use the factored form of a quadratic equation:
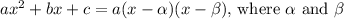`\( ax^2 + bx + c = a(x - \alpha)(x - \beta) \), where \( \alpha \) and \( \beta \)` are the zeroes. In this case, the zeroes are
`\( (3)/(5) - (3)/(5)i \) and \( (3)/(5) + (√(3))/(5) \).`

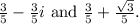
The factored form would be
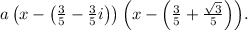`\( a\left(x - \left((3)/(5) - (3)/(5)i\right)\right)\left(x - \left((3)/(5) + (√(3))/(5)\right)\right) \).`Simplifying this expression gives the quadratic polynomial
`\( x^2 - (3)/(5)x + (27)/(25) \).`

Therefore, the correct answer is Option D,
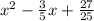`\( x^2 - (3)/(5)x + (27)/(25) \)`, which accurately represents the quadratic polynomial with the specified zeroes.

Options A, B, and C do not match the required form, making them incorrect choices. Understanding the relationship between zeroes and the factored form of a quadratic equation is essential to determine the correct answer.