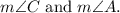Final Answer:
Given:
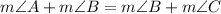
Prove:

Step-by-step explanation:
The given expression
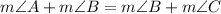 suggests that the measure of angle \(A\) combined with the measure of angle B is equal to the sum of the measures of angles B and C.
suggests that the measure of angle \(A\) combined with the measure of angle B is equal to the sum of the measures of angles B and C.
By subtracting
 )from both sides of the equation, we get
)from both sides of the equation, we get
 , which implies that the measure of angle Cis equal to the measure of angle \(A\).
, which implies that the measure of angle Cis equal to the measure of angle \(A\).
In conclusion, the statement is proven, and we can now assert that
 . This deduction is based on the assumption that the sum of the measures of angles A and B is equal to the sum of the measures of anglesB and C. The algebraic manipulation establishes the equality of
. This deduction is based on the assumption that the sum of the measures of angles A and B is equal to the sum of the measures of anglesB and C. The algebraic manipulation establishes the equality of