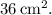Question

If a cube has a volume of 216cm than what is the area of the shaded face

Answer 1

The area of the shaded face of the cube is
`\(36 \, \text{cm}^2\).`

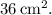
To determine the area of the shaded face of a cube with a volume of 216 cubic centimeters, let's first find the length of one side s of the cube.

The volume (V) of a cube is given by the formula
`\(V = s^3\)`.

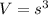Given that V = 216, we can solve for \(s\):

`\[216 = s^3\]`

Taking the cube root of both sides:

s = 6

Now that we know (s), the area (A) of any face of the cube is given by
`\(A = s^2\).`

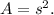
Therefore, the area of the shaded face is:

`\[A = 6^2 = 36 \, \text{cm}^2\]`

So, the area of the shaded face of the cube is
`\(36 \, \text{cm}^2\).`