Question

Convert 4(cos(120°) + isin(120°) into rectangular form.​

Answer 1

To convert from polar to rectangular form, the coordinates are determined by multiplying the polar radius by the cosine and sine of the angle respectively. For 4(cos(120°) + isin(120°)), the conversion results in the rectangular form of -2 + 2√3i.

Step-by-step explanation:

To convert 4(cos(120°) + isin(120°)) into rectangular form, we use the fact that cos(120°) and sin(120°) give us the x and y coordinates (respectively) in the rectangular (or Cartesian) coordinate system.

The angle 120° is in the second quadrant, where the cosine is negative and the sine is positive.

The values are: cos(120°) = -1/2 and sin(120°) = √3/2.

Multiplying these by 4, we get 4 * -1/2 = -2 for the x-coordinate and 4 * √3/2 = 2√3 for the y-coordinate.

Therefore, the rectangular form is -2 + 2√3i.

Answer 2

To convert from polar to rectangular form, the coordinates are determined by multiplying the polar radius by the cosine and sine of the angle respectively. For 4(cos(120°) + isin(120°)), the conversion results in the rectangular form of -2 + 2√3i.

Step-by-step explanation:

To convert
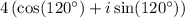`\(4\left(\cos(120^\circ) + i\sin(120^\circ)\right)\)` into rectangular form, we use Euler's formula,
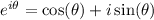`\(e^(i\theta) = \cos(\theta) + i\sin(\theta)\)`. Here,
`\(120^\circ\)` is our angle, so we have
`\(e^(i120^\circ)\)`.

Step 1: Evaluate the trigonometric functions at
`\(120^\circ\)`:

`\[ \cos(120^\circ) = -(1)/(2) \]`

`\[ \sin(120^\circ) = (√(3))/(2) \]`

Step 2: Substitute these values into Euler's formula:

`\[4 \left( -(1)/(2) + i(√(3))/(2) \right)\]`

This gives us the rectangular form of the complex number. For 4(cos(120°) + isin(120°)), the conversion results in the rectangular form of -2 + 2√3i.

Euler's formula is a powerful tool in complex number representation, enabling the conversion between polar and rectangular forms. Understanding this formula is fundamental in various mathematical and engineering applications, including signal processing and control systems.