Answer:
Likely Xenon,
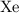 .
.
Step-by-step explanation:
The average kinetic energy of particles of a gas at a given temperature and pressure should be the same (regardless of the exact composition of the particle.)
For example, let
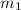 and
and
 denote the mass of each particle of two gases, and let
denote the mass of each particle of two gases, and let
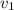 and
and
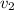 denote the average speed of particles of each gas.
denote the average speed of particles of each gas.
Average kinetic energy of particles of the first gas:
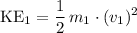 .
.
Average kinetic energy of particles of the second gas:
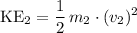 .
.
If the temperature of these two gases are the same,
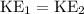 . Hence:
. Hence:
 .
.
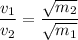 .
.
In other words, the average velocity of particles of each gas (at the same temperature and pressure) is inversely proportional to the square root of the mass of one particle of each gas.
Similarly, at the same temperature and pressure, particles of the four gases in this question would have the same average kinetic energy. However, the gas with the largest per-particle mass would have the slowest average velocity for its particles.
Look up the relative atomic mass of the particles:
Calculate the formula mass of each gas. That value would be proportional to the average mass of each particle of the gas:
Among these four gases, each particle of xenon,
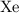 , has the largest per-particle mass. Hence, at the same temperature and pressure, particles of Xenon would have the slowest average velocity among these gases.
, has the largest per-particle mass. Hence, at the same temperature and pressure, particles of Xenon would have the slowest average velocity among these gases.