The length of the arc FG is
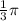 .
.
In a circle, the area of a sector can be related to the area of the whole circle using the formula:
![\[ \text{Area of sector} = \left( \frac{\text{measure of central angle}}{360^\circ} \right) * \pi r^2 \]](https://img.qammunity.org/2024/formulas/mathematics/college/yzt68659arh3glu0do8kbbedgfsqu4utiw.png)
where r is the radius of the circle.
In this case, you are given that
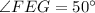 and the area of the shaded sector is
and the area of the shaded sector is
 . Let r be the radius of the circle.
. Let r be the radius of the circle.
![\[ \text{Area of sector} = (50^\circ)/(360^\circ) * \pi r^2 = (5)/(4)\pi \]](https://img.qammunity.org/2024/formulas/mathematics/college/ug1bp5kyclhnq5iwd2jsbdo69wdr36dgiz.png)
Now, solve for r :
![\[ (50)/(360) * \pi r^2 = (5)/(4)\pi \]](https://img.qammunity.org/2024/formulas/mathematics/college/xuldrw4m5amzuu9se7ebftjn6q24bz87lp.png)
Multiply both sides by
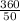 to solve for
to solve for
 :
:
![\[ \pi r^2 = (5)/(4) * (360)/(50) * \pi \]](https://img.qammunity.org/2024/formulas/mathematics/college/pgr3l5l0wgl7r3jvprl3tgxtv3zkcdq8ge.png)
Simplify:
![\[ r^2 = (9)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/college/6nm9h1tbe8u08yla3bkco35mkr2ab8bcpx.png)
Now, find the length of the arc FG. The formula for the length of an arc, given the central angle in degrees
 and the radius r, is:
and the radius r, is:
![\[ \text{Arc Length} = \left( (\theta)/(360^\circ) \right) * 2\pi r \]](https://img.qammunity.org/2024/formulas/mathematics/college/m2rg2hwzsk0jxl8vuvuaknwfukstrm2sum.png)
In this case,
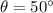 and
and
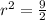 , so
, so
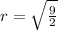 .
.
![\[ \text{Arc Length} = (50)/(360) * 2\pi \sqrt{(9)/(2)} \]](https://img.qammunity.org/2024/formulas/mathematics/college/dskbkgxv2f774h29qmjocb6o7krvjkzn8x.png)
Simplify:
![\[ \text{Arc Length} = (1)/(9) \pi √(18) \]](https://img.qammunity.org/2024/formulas/mathematics/college/6epaccxag6a1fpebe60oznqp2hu7omx5sy.png)
Expressing this in the form of a fraction times
 :
:
![\[ \text{Arc Length} = (1)/(9) * 3\pi = (1)/(3)\pi \]](https://img.qammunity.org/2024/formulas/mathematics/college/7wzkn5hnxkxsrmzkfhb2af7u5l37xlreza.png)
Therefore, the length of the arc FG is
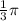 .
.