=>> Solution (part A) :
Given :
▪︎Triangle AMG is an isosceles triangle.
▪︎Measure of segment AM = (x+1.4) inches
▪︎Measure of segment MG = (2x+0.1) inches
▪︎Measure of segment AG = (3x-0.4) inches
▪︎segment AG is the base of triangle AMG.
Since AG is the base of the isosceles triangle AMG, segment AM and segment MG will be equal.
Which means :
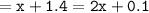

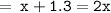


Thus, the value of x = 1.3
Therefore :
▪︎The value of x = 1.3
=>> Solution (Part B) :
We know that :
▪︎The value of x = 1.3
Which means :
The length of the leg AM :
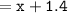
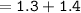

Thus, the length of the leg AM = 2.7 inches
The length of leg MG :
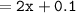
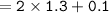
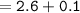

Thus, the length of the leg MG = 2.7 inches
Since the measure of the two legs are equal (2.7=2.7), we can conclude that we have found out the correct length of each leg.
Therefore :
▪︎Measure of leg AM = 2.7 inches
▪︎Measure of leg MG = 2.7 inches
=>> Solution (part C) :
We know that :
Value of x = 1.3
Then, measure of the base AG :


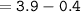
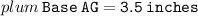
Thus, the measure of the base = 3.5 inches
Therefore :
▪︎ the length of base AG = 3.5 inches.