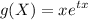The question is incomplete. The complete question is :
Let X be a random variable with probability mass function
P(X =1) =1/2, P(X=2)=1/3, P(X=5)=1/6
(a) Find a function g such that E[g(X)]=1/3 ln(2) + 1/6 ln(5). You answer should give at least the values g(k) for all possible values of k of X, but you can also specify g on a larger set if possible.
(b) Let t be some real number. Find a function g such that E[g(X)] =1/2 e^t + 2/3 e^(2t) + 5/6 e^(5t)
Solution :
Given :
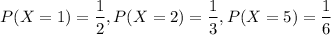
a). We know :
![$E[g(x)] = \sum g(x)p(x)$](https://img.qammunity.org/2022/formulas/mathematics/college/2s0drfk4clggttrzw67r9ygnm3hgyj8zta.png)
So,
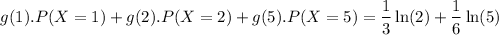

Therefore comparing both the sides,
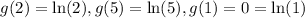
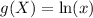
Also,
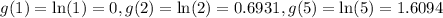
b).
We known that
![$E[g(x)] = \sum g(x)p(x)$](https://img.qammunity.org/2022/formulas/mathematics/college/2s0drfk4clggttrzw67r9ygnm3hgyj8zta.png)
∴
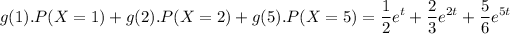
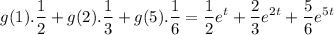
Therefore on comparing, we get
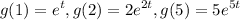
∴