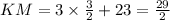**Problem 1:**

**Problem 2:**
-
 (Note: This result indicates that the given values may not form a valid triangle, as side lengths cannot be negative.)
(Note: This result indicates that the given values may not form a valid triangle, as side lengths cannot be negative.)
-
 (Note: This result indicates that the given values may not form a valid triangle, as side lengths cannot be negative.)
(Note: This result indicates that the given values may not form a valid triangle, as side lengths cannot be negative.)
-
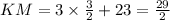
**Problem 1:**
Given triangle
 :
:
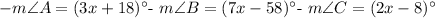
We know that the sum of the interior angles of a triangle is
 , so:
, so:
![\[ m\angle A + m\angle B + m\angle C = 180^\circ \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/478rl4czakk9c7xauo934kdihudfdtbpr4.png)
Substitute the given expressions:
![\[ (3x + 18) + (7x - 58) + (2x - 8) = 180 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/lps31c32h7v4q74q66t607135git8u78t5.png)
Combine like terms:
![\[ 12x - 48 = 180 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/a0nw0plh8toa5hhirx1b6o7hg5ve552zlv.png)
Add 48 to both sides:
![\[ 12x = 228 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/irsx58w3dwwhalhdmvoqgrlig87vtns0w5.png)
Divide by 12:
![\[ x = 19 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/x138n62x8qz7594rvckaghoqxwusmz20d0.png)
Now, substitute \(x\) back into the angle expressions:

**Problem 2:**
Given triangle
 :
:
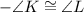
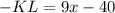
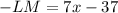
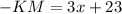
Since
 , it's an isosceles triangle, and the two sides opposite these angles are congruent. Therefore, KL = LM:
, it's an isosceles triangle, and the two sides opposite these angles are congruent. Therefore, KL = LM:
![\[ 9x - 40 = 7x - 37 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7nzto3g59ld9bf9c3tjw4t3lhm4d5kx9cj.png)
Subtract 7x from both sides:
![\[ 2x - 40 = -37 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/coi1mlci15w2cu993ct06uj4onedoeyvym.png)
Add 40 to both sides:
![\[ 2x = 3 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yvwube5aqyv212k9jzhg1ptes1krm8vs5u.png)
Divide by 2:
![\[ x = (3)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ongrfyn19zbx6dpth9ex2b5ot091x77svf.png)
Now, substitute x back into the expressions:
-
 (Note: This result indicates that the given values may not form a valid triangle, as side lengths cannot be negative.)
(Note: This result indicates that the given values may not form a valid triangle, as side lengths cannot be negative.)
-
 (Note: This result indicates that the given values may not form a valid triangle, as side lengths cannot be negative.)
(Note: This result indicates that the given values may not form a valid triangle, as side lengths cannot be negative.)
-