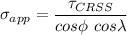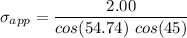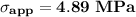Answer:
Step-by-step explanation:
From the given information:
The equation for applied stress can be expressed as:
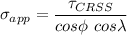
where;
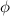 = angle between the applied stress [100] and [111]
= angle between the applied stress [100] and [111]
To determine the
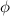 and
and
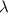 for the system
for the system
Using the equation:
![\phi= cos^(-1)\Big [(l_1l_2+m_1m_2+n_1n_2)/(√((l_1^2+m_1^2+n_1^2)(l_2^2+m_2^2+n_2^2)))\Big]](https://img.qammunity.org/2022/formulas/engineering/college/fi7b79kzgmrmkb3bw3060zqs6sstyw9aox.png)
for [100]
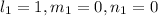
for [111]
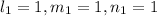
Thus;
![\phi= cos^(-1)\Big [(1*1+0*1+0*1)/(√((1^2+0^2+0^2)(1^2+1^2+1^2)))\Big]](https://img.qammunity.org/2022/formulas/engineering/college/54c3vl4xu3pjig9fbk26dtr489e2vog96g.png)
![\phi= cos^(-1)\Big [(1)/(√((3)))\Big]](https://img.qammunity.org/2022/formulas/engineering/college/217plvd1uhfcglw4h8v3fcyalekj2lviqf.png)
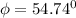
To determine
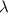 for
for
![[1 \overline 1 0]](https://img.qammunity.org/2022/formulas/engineering/college/3mq81ivgfsbe86fyighf5s6509o1c6qbp3.png)
where;
for [100]
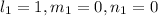
for
![[1 \overline 1 0]](https://img.qammunity.org/2022/formulas/engineering/college/3mq81ivgfsbe86fyighf5s6509o1c6qbp3.png)
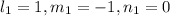
Thus;
![\lambda= cos^(-1)\Big [(1*1+0*1+0*0)/(√((1^2+0^2+0^2)(1^2+(-1)^2+0^2)))\Big]](https://img.qammunity.org/2022/formulas/engineering/college/9f97lph1fwpgyqttjjimlctty11s6owb7f.png)
![\phi= cos^(-1)\Big [(1)/(√((2)))\Big]](https://img.qammunity.org/2022/formulas/engineering/college/5ulq9cw3glwpvx7m5hs9fr95gt8wqkz9ns.png)
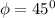
Thus, the magnitude of the applied stress can be computed as: