Question

Essentially, I want to know how much of a material (depth wise) I need to break the fall of an object while keeping that object below 9g's. I am planning on using a honeycomb core structure to break the fall like a crumple zone.

I know: My material for the crumple zone, the area it covers, velocity of falling object (constant), the weight of the falling object, and the time needed to decelerate without exceeding 9g's.

The main thing I am confused on is how to calculate how much depth of the material I need to give the object enough slowing time. Any help is appreciated especially useful equations!

Answer 1

To determine the depth of material needed, you can use the following equation:

`\[ d = (v^2)/(2a) \]`

where:

( d ) is the depth of the material,

( v ) is the velocity of the falling object,

(a) is the desired deceleration (in this case, 9g).

Step-by-step explanation:

The equation
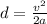`\( d = (v^2)/(2a) \)` comes from the kinematic equation
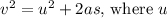`\( v^2 = u^2 + 2as \), where \( u \)` is the initial velocity (assumed to be zero as the object starts falling), s is the distance traveled, and a is the acceleration (negative in the deceleration phase).

In this scenario, you want to solve for
`\( s \)`, which is the depth of the material. Rearranging the equation gives
`\( s = (v^2)/(2a) \)`. To maintain a deceleration of 9g or
`\( 9 * 9.8 \, m/s^2 \),` you substitute
`\( a = -9 * 9.8 \)` in the formula. Given your specific velocity and deceleration requirements, this will provide the necessary depth of the honeycomb core structure.

It's important to note that this equation assumes constant deceleration, which may not be entirely accurate depending on the specifics of your design. Consider factors like the material's deformation characteristics and the possibility of non-uniform deceleration for a more detailed analysis. Additionally, always ensure safety margins in your design to account for uncertainties and variations.