Question

You are designing an automatic coin counter that stacks 50 pennies at a time to be placed in coin wrappers. You plan on measuring the height of the stack to determine the number of coins, but are concerned as to how accurate the method will be. You measure the thickness of 30 pennies, with the data listed at the left. a. Based on these data, estimate the height of a stack ofany50 pennies. How accurate is your estimate, at 95%confidence?

Answer 1

The question is incomplete. Here is the complete question.

You are designing an automatic coin counter that stacks 50 pennies at a time to be placed in coin wrappers. You plan on measuring the height of the stack to determine the number of coins, but are concerned as to how accurate the method will be. You measure the thickness of 30 penniesm with the data listed below.

a. Based on these data, estimate the height of a stack of any 50 pennies. How accurate is your estimate, at 95% confidence?

b. What percentage of pennies from the population have thickness of at least 1.34mm?

Answer: a. Height = 74.25mm with margin of error of 0.021.

b. 99.38%

Explanation:

a. To estimate the height of any 50 pennies, we have to determine the average of thickness of the sample given in the table.

Average is calculated as the sum of all the data divided by the quantity the sample has, so:

`\overline{x}=(\Sigma x)/(n)`

`\overline{x}=(44.56)/(30)`

`\overline{x}=1.485`

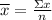
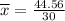
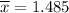
Each coin is estimated to have 1.485 mm of thickness. Then, the height of 50 pennies is

h = 1.485*50

h = 74.25

50 pennies will have an estimate height of 74.25 mm.

Margin of Error expresses the amount of random sampling error the results in a survey can have. It will show how many percentage points the result is from the actual population value.

To calculate it, we have to determine standard deviation of the data.

Standard deviation is

`s=\sqrt{\frac{\Sigma (x-\overline{x})^(2)}{n-1} }`

`s=\sqrt{(0.09735)/(29) }`

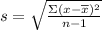
s = 0.058

For a 95% confidence, z-score is 1.96.

Margin is

`E=z.(s)/(√(n))`

`E=1.96((0.058)/(√(30)))`

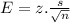
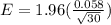
E = 0.021

The accuracy of the estimate is 2.1%.

b. The percentage of pennies with thickness at least 1.34mm is represented as P(x>1.34). To calculate it:

P(x>1.34) = 1 - P(x<1.34)

Now, we have to normalize the data:

`z=(x-\mu)/(\sigma)`

`z=(1.34-1.485)/(0.058)`

`z=-2.5`

`P(x<1.34)=P(z<-2.5)`

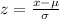
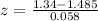
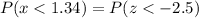
Consulting the z table,

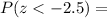`P(z<-2.5)=` 0.00621

Now, for the percentage:

`P(x>1.34)=1-0.00621`

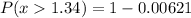
P(x > 1.34) = 0.9938 or 99.38%

The percentage of pennies with thickness of at least 1.34mm is 99.38%.