Answer:
The difference between the principal and the compound interest in three years is Rs 17,994
Explanation:
The compound interest is given according to the following formula;
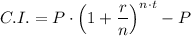
The given amount of the compound after 2 years = Rs 5,460
The given amount of the compound after 4 years = Rs 12,066.60
Therefore, we have;
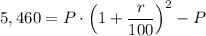 ...(1)
...(1)
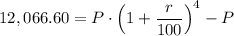 ...(2)
...(2)
Dividing equation (2) by (1), we have;
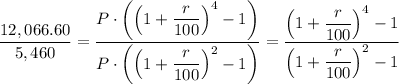
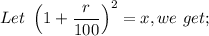
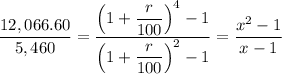
∴ 12,066.60 × (x - 1) = 5,460 × (x² - 1) = 5,460 × (x - 1) ×(x + 1)
∴ 12,066.60 × (x - 1)/(x - 1) = 5,460 × (x + 1)
12,066.60/5,460 = x + 1
x = 12,066.60/5,460 - 1 = 1.21 = 121/100
x = 121/100
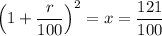
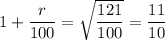
We get
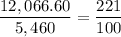


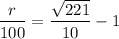
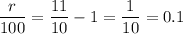
r = 100 × 0.1 = 10%
r = 10%
Therefore, we have;
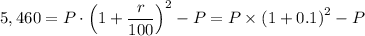
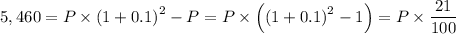
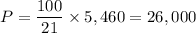
The principal = Rs. 26,000
The compound interest in 3 years is therefore;
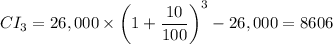
The difference, 'd', between the principal and the compound interest in three years, is given as follows;
d = P - CI₃
d = 26,600 - 8606 = 17994
The difference between the principal and the compound interest in three years, d = Rs 17,994.