Answer:
since p-value (0.0801) is < 0.10, the result is significant
so, we reject Null hypothesis
Explanation:
Given the data in the question;
Null Hypothesis H₀ : p = 0.27
Alternative Hypothesis H₁ : p ≠ 0.27
Test statistic
z = (
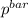 - p)/√(
- p)/√(
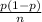 )
)
we substitute
z = (0.25 - 0.27)/√(
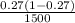 )
)
z = -0.02 / √( 0.1971/1500)
z = -0.02 / 0.01146
z = -1.7452 ≈ -1.75
p-value;
for z = -1.75, the two tailed p value is 0.0801
Decision
since p-value (0.0801) is < 0.10, the result is significant
so, we reject Null hypothesis