Question

Constructive interference is observed from directly above an oil slick for wavelengths (in air) 440 nm and 616 nm. The index of refraction of this oil is n=1.54. What is the film’s minimum possible thickness?

Answer 1

The minimum film thickness for constructive interference at both 440 nm and 616 nm, in a film with n=1.54, is found to be 286 nm. This is the first common multiple of the fundamental constructive interference thicknesses for both wavelengths.

Step-by-step explanation:

Calculation of Minimum Film Thickness

To calculate the film's minimum possible thickness for constructive interference at the given wavelengths, we apply the formula for thin film interference. The condition for constructive interference in a thin film is given by:

`2nt = m \( \lambda \),`

where n is the index of refraction of the film, t is the thickness of the film,
`\( \lambda \)`is the wavelength of light in vacuum/air, and m is an integer representing the order number of the interference.

For the first order (m=1) constructive interference:

`t = \( (\lambda)/(2n) \)`

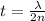
Plugging in the values for the shortest wavelength (440 nm) and the index of refraction of the oil (n=1.54), we get:

`t = \( (440 nm)/(2 * 1.54) \)`

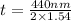
= 143 nm.

For higher order (m>1) interference, the thickness would have to be a multiple of this fundamental thickness. As we look for the minimum possible thickness that would cause constructive interference for both wavelengths, we have to consider the possibility that the higher wavelength is on a higher order interference. Therefore, we check for a shared multiple:

• The second wavelength (616 nm) for the first order (m=1) would imply
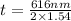  `t = \( (616 nm)/(2 * 1.54) \)` = 200 nm, which is not a multiple of the thickness calculated for the shorter wavelength.
• For the second order (m=2) of the shorter wavelength (440 nm),
  `t = \( (2 * 440 nm)/(2 * 1.54) \) = 286 nm.`

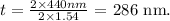
By comparing these results, we can determine that 286 nm would be the minimum possible thickness that satisfies constructive interference conditions for both given wavelengths as it is the lowest common multiple.