The box at the right is a cube with edges that measure 2 feet. The sides of the triangle inside the cube are a diagonal of a face, an edge, and a segment with endpoints at opposite corners of the cube. The triangle is a right triangle with leg lengths 2 and
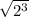
. Write the area of the triangle as the number 2 with a rational exponent.