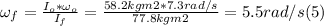Question

A thin uniform cylindrical turntable of radius 2.3 m and mass 22 kg rotates in a horizontal plane with an initial angular speed of 7.3 rad/s. The turntable bearing is frictionless. A clump of clay of mass 8.7 kg is dropped onto the turntable and sticks at a point 1.5 m from the point of rotation. Treat the clay as a point mass. Find the angular speed of the clay and turntable. Answer in units of rad/s.

Answer 1

ω = 5.5 rad/s

Step-by-step explanation:

• Assuming no external torques present during the instant that the clump of clay is dropped on the turntable, total angular momentum must be conserved.
• The angular momentum of a rotating rigid body, can be expressed as follows:

`L = I * \omega (1)`

where I = moment of inertia regarding the axis of rotation, and ω =

angular speed of the rotating body.

• Since the angular momentum must keep constant, this means that it must be satisfied the following equality:

`L_(o) = L_(f) (2)`

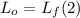
where L₀ = I₀ * ω₀, Lf = If * ωf.

I₀ is the moment of inertia of a solid disk rotating around an axis

passing through its center, as follows:

`I_(o) =(1)/(2) * m* r^(2) = (1)/(2) * 22 kg*(2.3m)^(2) = 58.2 kgm2 (3)`

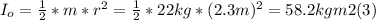
If, is the moment of inertia after dropping the clump of clay, which adds

its own moment of inertia as a point mass, as follows:

`I_(f) =(1)/(2) * m* r^(2) + m_(cl) * r_(cl)^(2) =58.2 kgm2 + (8.7kg)*(1.5m)^(2) \\ = 58.2 kgm + 19.6 kgm2 = 77.8 kgm2 (4)`

• Replacing I₀, If and ω₀ in (2), we can solve for ωf, as follows:

`\omega_(f) = (I_(o) *\omega_(o) )/(I_(f)) = (58.2kgm2*7.3rad/s)/(77.8kgm2) = 5.5 rad/s (5)`