Question

What is the radius of a circle whose equation is (x+5) ^2+(y-3)^2=4^2

2 units
4 units
8 units
16 units

Answer 1

Based on the equation
`(x + 5)^2 + (y - 3)^2 = 4^2`, we can conclude that the center of the circle is (-5, 3) and the radius is 4 units.

In the given equation,
`(x + 5)^2 + (y - 3)^2 = 4^2`, we can compare it to the standard form of a circle equation,
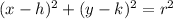`(x - h)^2 + (y - k)^2 = r^2`. This standard form represents a circle with center (h, k) and radius r.

1. Center of the circle: By comparing the given equation to the standard form, we can determine that the center of the circle is (-5, 3). The value inside the parentheses of x represents the horizontal shift of the center, and the value inside the parentheses of y represents the vertical shift of the center.

2. Radius of the circle: The value on the right side of the equation,
`4^2`, represents the square of the radius. To find the actual radius, we need to take the square root of
`4^2`, which is 4.

Therefore, based on the equation
`(x + 5)^2 + (y - 3)^2 = 4^2`, we can conclude that the center of the circle is (-5, 3) and the radius is 4 units.