Answer:
Explanation:
From the given information;
The present value of series A:
![=\Big[1000 * ((1.095)^0)/((1.09)^1)\Big]+\Big[1000 * ((1.095)^1)/((1.09)^2)\Big]+...+\Big[1000 * ((1.095)^4)/((1.09)^5)\Big]](https://img.qammunity.org/2022/formulas/mathematics/college/6dkqqe7r1a4899hwpvxsvehpy765tu2d17.png)
![= 1000 \Big [ (1)/(1.09)+ (1.095)/(1.1881)+ (1.199)/(1.295)+(1.313)/(1.912)+(1.438)/(1.539)\Big]](https://img.qammunity.org/2022/formulas/mathematics/college/3twk5wl23noeqcon8nnumzlaiwhahjz2m9.png)
![= 1000 \Big[ 0.917 + 0.922 + 0.926 + 0.930 + 0.934\Big]](https://img.qammunity.org/2022/formulas/mathematics/college/ansqt25o47z5rbdq8nhe7wxjntzpi7jqwa.png)
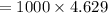
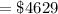
Thus, the present value of series A is = $4629
Present value of series A = Present value of series B
![The \ value \ of\ X = (Present \ value \ of \ series \ B )/(\Big [(1-(1+r)^(-n))/(r) \Big ])](https://img.qammunity.org/2022/formulas/mathematics/college/gczz5ct2bd2cls1w3ensskec31x4em2yw5.png)
![The \ value \ of\ X = (4629 )/(\Big [(1-(1+0.09)^(-5))/(0.09) \Big ])](https://img.qammunity.org/2022/formulas/mathematics/college/cnvam1494t9pimolm9n274zy7pfjepdfic.png)
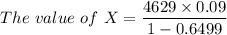
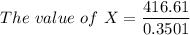
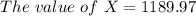
Thus, the value of X = $1189.97
2.
The present value of series A:
![=1000 * \Big[((1.095)^0)/((1.08)^1)+ ((1.095)^1)/((1.08)^2)+...+((1.095)^4)/((1.08)^5)\Big]](https://img.qammunity.org/2022/formulas/mathematics/college/mgmwamt1gv7x9ig6vfwrjj30da2c91p86o.png)
![=1000 \Big [ (1)/(1.08)+ (1.095)/(1.1664)+(1.199)/(1.2597)+(1.313)/(1.3605)+(1.438)/(1.4693)\Big ]](https://img.qammunity.org/2022/formulas/mathematics/college/gyje95ml0kevrmfu1b5fds0ink1zhxphuu.png)
![= 1000\Big [ 0.9259 + 0.9839+0.952 + 0.965+0.979\Big ]](https://img.qammunity.org/2022/formulas/mathematics/college/15r5cjxlntlqtoduot8nun1d7245jxi7bh.png)
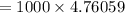
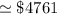
Thus, the present value of series A is = $4761
Present value of series B =
![Value \ of \ X * \Big [ (1 - (1+r)^(-n) )/(r)\Big ]](https://img.qammunity.org/2022/formulas/mathematics/college/cfav1nhzfujcayxi8f2gxqpbqxlkrxiuii.png)
![= 1189.97 * \Big [ (1 - (1+0.08)^(-5) )/(0.08)\Big ]](https://img.qammunity.org/2022/formulas/mathematics/college/dcktj1yhw360nwdpw2vpeotk8fwziq29vg.png)
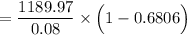
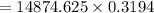
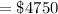
Thus, the present value of series B = $4750
3.
The present value of series A:
![=1000 * \Big[((1.095)^0)/((1.05)^1)+ ((1.095)^1)/((1.05)^2)+...+((1.095)^4)/((1.05)^5)\Big]](https://img.qammunity.org/2022/formulas/mathematics/college/paw06llebzxq7800vdknbi15l09rknjwws.png)
![=1000 \Big [ (1)/(1.05)+ (1.095)/(1.1025)+(1.199)/(1.1576)+(1.313)/(1.2155)+(1.438)/(1.276)\Big ]](https://img.qammunity.org/2022/formulas/mathematics/college/cj4u35n6bfrjfiatpwiwd08sig1mny2ff0.png)
![= 1000\Big [ 0.9524 + 0.9932+1.0357 + 1.08+1.127\Big ]](https://img.qammunity.org/2022/formulas/mathematics/college/85km2d7q6t6bly2vhysoss5eiok9ur9uzc.png)
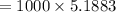
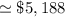
Thus, the present value of series A = $5188
Present value of series B: =
![Value \ of \ X * \Big [ (1 - (1+r)^(-n) )/(r)\Big ]](https://img.qammunity.org/2022/formulas/mathematics/college/cfav1nhzfujcayxi8f2gxqpbqxlkrxiuii.png)
![= 1189.97 * \Big [ (1 - (1+0.05)^(-5) )/(0.05)\Big ]](https://img.qammunity.org/2022/formulas/mathematics/college/dmfq85gammydu64o9xmxr6ulld92e3ua11.png)
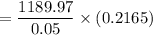
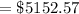
Thus, the present value of series B = $5153