Question

Consider the following two cash flow series of payments: Series A is a geometric series increasing at a rate of 9.5% per year. The initial cash payment at the end of year 1 is $1,000. The payments occur annually for 5 years. Series B is a uniform series with payments of value X occurring annually at the end of years 1 through 5. You must make the payments in either Series A or Series B.

a. Determine the value of X for which these two series are equivalent if your TVOM is i = 9%. $
b. If your TVOM is 8%, would you be indifferent between these two series of payments? Enter the PW for each series to support this choice.
c. If your TVOM is 5%, would you be indifferent between these two series of payments? Enter the PW for each series to support this choice.

Answer 1

Explanation:

From the given information;

The present value of series A:
`=\Big[1000 * ((1.095)^0)/((1.09)^1)\Big]+\Big[1000 * ((1.095)^1)/((1.09)^2)\Big]+...+\Big[1000 * ((1.095)^4)/((1.09)^5)\Big]`

`= 1000 \Big [ (1)/(1.09)+ (1.095)/(1.1881)+ (1.199)/(1.295)+(1.313)/(1.912)+(1.438)/(1.539)\Big]`

`= 1000 \Big[ 0.917 + 0.922 + 0.926 + 0.930 + 0.934\Big]`

`= 1000 * 4.629`

`= \$4629`

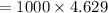
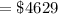
Thus, the present value of series A is = $4629

Present value of series A = Present value of series B

`The \ value \ of\ X = (Present \ value \ of \ series \ B )/(\Big [(1-(1+r)^(-n))/(r) \Big ])`

`The \ value \ of\ X = (4629 )/(\Big [(1-(1+0.09)^(-5))/(0.09) \Big ])`

`The \ value \ of\ X =(4629 * 0.09)/(1-0.6499)`

`The \ value \ of\ X =(416.61)/(0.3501)`

`The \ value \ of\ X =1189.97`

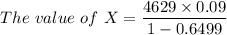
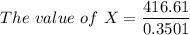
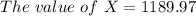
Thus, the value of X = $1189.97

2.

The present value of series A:

`=1000 * \Big[((1.095)^0)/((1.08)^1)+ ((1.095)^1)/((1.08)^2)+...+((1.095)^4)/((1.08)^5)\Big]`

`=1000 \Big [ (1)/(1.08)+ (1.095)/(1.1664)+(1.199)/(1.2597)+(1.313)/(1.3605)+(1.438)/(1.4693)\Big ]`

`= 1000\Big [ 0.9259 + 0.9839+0.952 + 0.965+0.979\Big ]`

`= 1000 * 4.76059`

`\simeq \$4761`

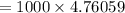
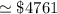
Thus, the present value of series A is = $4761

Present value of series B =
`Value \ of \ X * \Big [ (1 - (1+r)^(-n) )/(r)\Big ]`

`= 1189.97 * \Big [ (1 - (1+0.08)^(-5) )/(0.08)\Big ]`

`= (1189.97)/(0.08) * \Big ( 1 -0.6806\Big )`

`= 14874.625 * 0.3194`

`= \$4750`

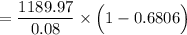
Thus, the present value of series B = $4750

3.

The present value of series A:

`=1000 * \Big[((1.095)^0)/((1.05)^1)+ ((1.095)^1)/((1.05)^2)+...+((1.095)^4)/((1.05)^5)\Big]`

`=1000 \Big [ (1)/(1.05)+ (1.095)/(1.1025)+(1.199)/(1.1576)+(1.313)/(1.2155)+(1.438)/(1.276)\Big ]`

`= 1000\Big [ 0.9524 + 0.9932+1.0357 + 1.08+1.127\Big ]`

`= 1000 * 5.1883`

`\simeq \$5,188`

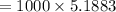
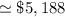
Thus, the present value of series A = $5188

Present value of series B: =
`Value \ of \ X * \Big [ (1 - (1+r)^(-n) )/(r)\Big ]`

`= 1189.97 * \Big [ (1 - (1+0.05)^(-5) )/(0.05)\Big ]`

`= (1189.97)/(0.05) *( 0.2165)`

`= \$5152.57`

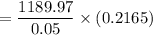
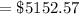
Thus, the present value of series B = $5153