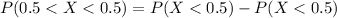Answer:
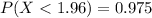
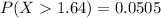

Explanation:
Given
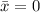 --- Mean
--- Mean
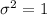 --- Variance
--- Variance
Calculate the standard deviation
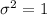
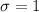
Solving (a): P(X < 1.96)
First, we calculate the z score using:
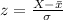
This gives:
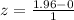
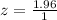
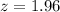
The probability is then solved using:
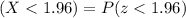
From the standard normal distribution table
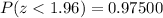
So:
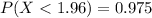
Solving (b): P(X > 1.64)
First, we calculate the z score using:
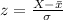
This gives:
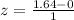
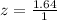
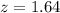
The probability is then solved using:
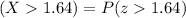
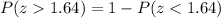
From the standard normal distribution table
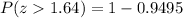
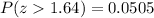
So:
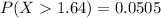
Solving (c): P(0.5 < X < 0.5)
This can be split as:
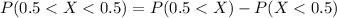
In probability:

![P(0.5<X) = 1 - [1 - P(X<0.5)]](https://img.qammunity.org/2022/formulas/mathematics/college/x0mh7mhgmtl1rpp0ueq368updqy7ectg5v.png)

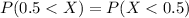
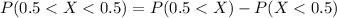 becomes
becomes