Answer:
a. Vc = 5.06 m/s
b. Vp = 22.18 m/s
Step-by-step explanation:
The acceleration of the pulley-mass system is as follows:
a =

Solving for acceleration, we get:
a =

a = 0.97
So, for the part a:
Calculate the velocity of the crewman by using the following equation:
Vc =
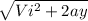
Substituting the values into the equation, we get:
Vc =

Vc = 5.06 m/s
Now, for part b:
Calculate the final velocity of the pulley by using the following expression:
Vp =
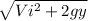
Just plugging in the values.
Vp =
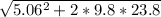
Vp = 22.18 m/s