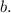Question

Snow fell at the same rate for two separate snow storms. During the storms, Raven measured the

depth of snow on the ground for each hour.
The depth of snow on the ground for Storm 1 is
Proportional relationship because
there were 0 inches of snow on the ground at
the start of the storm.
What is the equation representing Storm 1?
The depth of snow on the ground for Storm 2 is
relationship because
there were 5 inches of snow on the ground at
the start of the storm.
What is the equation representing Storm 2?
Depth of Snow (inches)
CO
6
2
0
(2,6)
(2, 1)
2
(4,7)
Summary Question
How do you use a graph to write the equation of a line using y = mx + b?
Storm 2
(4,2)
Storm 1
3
5
6
4
7
Time Since Start of Storm (hours

Answer 1

For Storm 1, with 0 inches of initial snow, the equation is
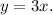`\(y = 3x\).` For Storm 2, starting with 5 inches, the equation is
`\(y = -2x + 5\)`, using slope-intercept form.

To find the equation representing the depth of snow on the ground for each storm, you can use the formula for a linear relationship, which is given by the equation
`\(y = mx + b\),` where:

-
`\(y\)` is the dependent variable (depth of snow),

-
`\(x\)` is the independent variable (time since the start of the storm),

-
`\(m\)` is the slope of the line, and

-
`\(b\)` is the y-intercept (the initial depth of snow).

For Storm 1, the depth of snow on the ground is 0 inches at the start of the storm (when \(x = 0\)). Therefore, the equation for Storm 1 is
`\(y = mx\).`

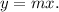
For Storm 2, the depth of snow on the ground is 5 inches at the start of the storm
`(when \(x = 0\)).` Therefore, the equation for Storm 2 is
`\(y = mx + 5\).`

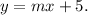
Now, let's find the slope
`(\(m\))` for both storms using the given data points.

For Storm 1:

- Points: (0, 0), (2, 6)

- Slope
`(\(m\))` =
`\(\frac{\text{Change in } y}{\text{Change in } x} = (6 - 0)/(2 - 0) = 3\)`

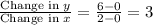
So, the equation for Storm 1 is
`\(y = 3x\).`

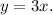
For Storm 2:

- Points: (0, 5), (2, 1)

- Slope
`(\(m\)) = \(\frac{\text{Change in } y}{\text{Change in } x} = (1 - 5)/(2 - 0) = -2\)`

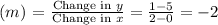
So, the equation for Storm 2 is
`\(y = -2x + 5\).`

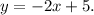
To use a graph to write the equation of a line using
`\(y = mx + b\):`

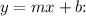
1. Plot the given points on the graph.

2. Calculate the slope
`(\(m\))` using the formula
`\(\frac{\text{Change in } y}{\text{Change in } x}\).`

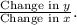
3. Determine the y-intercept
`(\(b\))` from the graph (the value of
`\(y\)` when
`\(x = 0\)).`

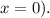
4. Write the equation
`\(y = mx + b\)` using the determined
`\(m\)` and
`\(b\).`