Question

Is achieving a basic skill level related to the location of the school? The results

of a random sample of students by the location of school and the number of
students achieving basic skill levels in three subjects is shown in the
contingency table. At a=0.10, test the hypothesis that the variables are
independent. Complete parts (a) through (d).
0.1.2
Find the critical value.
x=4.605
(Round to three decimal places as needed.)
Choose the correct rejection region below.
As%²
B. ?>x
c.x²2x²
●D.x²2² (c) Calculate the test statistic. If convenient, use technology.
(Round to two decimal places as needed.)
Subject
Location Reading Math Science
Urban 49 42 37
Suburban 63 62 51

Answer 1

1. **Critical Value:** x = 4.605

2. **Rejection Region:**
`\( x^2 > x \)`

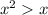
3. **Test Statistic (
`\(\chi^2\)`):** 4.036

4. **Conclusion:** Fail to reject the null hypothesis, suggesting no significant relationship between school location and basic skill level achievement at the 0.10 significance level.

To test the hypothesis that the variables (location of the school and achievement of basic skill levels) are independent, we use the chi-square (
`\(\chi^2\)`) test. Here are the steps:

**a. Critical Value:**

- Given significance level
`\(\alpha = 0.10\)` with 2 degrees of freedom (since we have 2 categories for location - Urban and Suburban), we look up the critical value in the chi-square distribution table.

- The critical value (x) is approximately 4.605.

**b. Rejection Region:**

- The rejection region is where the test statistic (
`\(\chi^2\)`) is greater than the critical value.

- The correct rejection region is
`\(x^2 > x\).`

**c. Test Statistic:**

- The test statistic is calculated using the formula:

`\[ \chi^2 = \sum ((O_(ij) - E_(ij))^2)/(E_(ij)) \]`

where
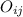`\(O_(ij)\)` is the observed frequency and
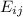`\(E_(ij)\)` is the expected frequency for each cell.

- Use technology to calculate this. If you use a calculator or statistical software, you will find
`\(\chi^2 \approx 4.036\).`

**d. Conclusion:**

- Compare the test statistic (
`\(\chi^2\)`) with the critical value. If
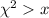`\(\chi^2 > x\)`, reject the null hypothesis that the variables are independent.

- In this case, 4.036 < 4.605, so we do not reject the null hypothesis.

**Final Answers:**

- Critical Value (x): 4.605

- Rejection Region:
`\(x^2 > x\)`

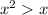
- Test Statistic (
`\(\chi^2\)`): 4.036

Therefore, based on the test, there is not enough evidence at the 0.10 significance level to conclude that the location of the school and achievement of basic skill levels are dependent.