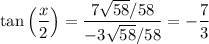Question

I need help with finding the answer to a) and b). Thank you!

Answer 1

`\displaystyle \sin\Big((x)/(2)\Big) = (7√(58) )/( 58 )`

`\displaystyle \cos\Big((x)/(2)\Big)=-(3 √(58))/(58)`

`\displaystyle \tan\Big((x)/(2)\Big)=-(7)/(3)`

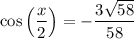
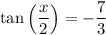
Explanation:

We are given that:

`\displaystyle \sin(x)=-(21)/(29)`

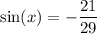
Where x is in QIII.

First, recall that sine is the ratio of the opposite side to the hypotenuse. Therefore, the adjacent side is:

`a=√(29^2-21^2)=20`

So, with respect to x, the opposite side is 21, the adjacent side is 20, and the hypotenuse is 29.

Since x is in QIII, sine is negative, cosine is negative, and tangent is also negative.

And if x is in QIII, this means that:

`180<x<270`

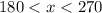
So:

`\displaystyle 90 < (x)/(2) < 135`

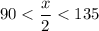
Thus, x/2 will be in QII, where sine is positive, cosine is negative, and tangent is negative.

1)

Recall that:

`\displaystyle \sin\Big((x)/(2)\Big)=\pm\sqrt{(1 - \cos(x))/(2)}`

Since x/2 is in QII, this will be positive.

Using the above information, cos(x) is -20/29. Therefore:

`\displaystyle \sin\Big((x)/(2)\Big)=\sqrt{(1 + 20/29)/(2)`

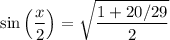
Simplify:

`\displaystyle \sin\Big((x)/(2)\Big)=\sqrt{(49/29)/(2)}=\sqrt{(49)/(58)}=(7)/(√(58))=(7√(58))/(58)`

2)

Likewise:

`\displaystyle \cos \Big( (x)/(2) \Big) =\pm \sqrt{ (1+\cos(x))/(2) }`

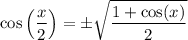
Since x/2 is in QII, this will be negative.

Using the above information, cos(x) is -20/29. Therefore:

`\displaystyle \cos \Big( (x)/(2) \Big) =-\sqrt{ (1- 20/29)/(2) }`

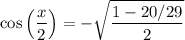
Simplify:

`\displaystyle \cos\Big((x)/(2)\Big)=-\sqrt{(9/29)/(2)}=-\sqrt{(9)/(58)}=-(3)/(√(58))=-(3√(58))/(58)`

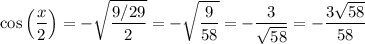
3)

Finally:

`\displaystyle \tan\Big((x)/(2)\Big) = (\sin(x/2))/(\cos(x/2))`

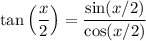
Therefore:

`\displaystyle \tan\Big((x)/(2)\Big)=(7√(58)/58)/(-3√(58)/58)=-(7)/(3)`