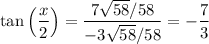Answer:
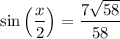
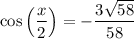
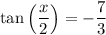
Explanation:
We are given that:
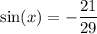
Where x is in QIII.
First, recall that sine is the ratio of the opposite side to the hypotenuse. Therefore, the adjacent side is:
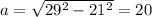
So, with respect to x, the opposite side is 21, the adjacent side is 20, and the hypotenuse is 29.
Since x is in QIII, sine is negative, cosine is negative, and tangent is also negative.
And if x is in QIII, this means that:
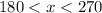
So:
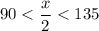
Thus, x/2 will be in QII, where sine is positive, cosine is negative, and tangent is negative.
1)
Recall that:
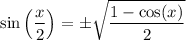
Since x/2 is in QII, this will be positive.
Using the above information, cos(x) is -20/29. Therefore:
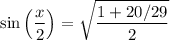
Simplify:
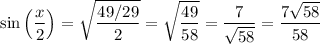
2)
Likewise:
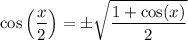
Since x/2 is in QII, this will be negative.
Using the above information, cos(x) is -20/29. Therefore:
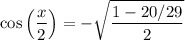
Simplify:
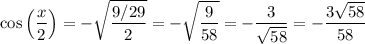
3)
Finally:
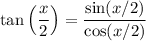
Therefore: