the farmer's entire orchard is
 acres.
acres.
Let x be the total number of acres in the farmer's orchard.
The information given states that
 acres of green apple trees make up
acres of green apple trees make up
 of the entire orchard.
of the entire orchard.
So, we can set up the equation:
![\[ 7(1)/(4) = (3)/(8) \cdot x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/k8qtyqhgdrsr00dqxte1o6e4nznbnti44q.png)
To simplify, convert
 to an improper fraction:
to an improper fraction:
![\[ (29)/(4) = (3)/(8) \cdot x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/eghhxp7sn9fje940pmr8w1o0wrnk3grx7b.png)
Now, to solve for x, multiply both sides of the equation by the reciprocal of
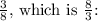
![\[ x = (29)/(4) \cdot (8)/(3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ycbsl3wzupurthmbednth0gq95pau809br.png)
Multiply the numerators and denominators:
![\[ x = (29 \cdot 8)/(4 \cdot 3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1ilvbtjh6rmi749yvnhumos9zk5omdhlzn.png)
![\[ x = (232)/(12) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jagd24y1rpqyqve7fopbxfez2kfwelcsk1.png)
Simplify the fraction:
![\[ x = 19(4)/(12) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4vzadqveh3zb7qh5744mhe2pbvoo0japzd.png)
![\[ x = 19(1)/(3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1iytlgzvoi2r4lb8sbe7de6mm2vnkyhs2w.png)
Therefore, the farmer's entire orchard is
 acres.
acres.
The probable question may be:
A farmer plants 7(1)/(4) acres of green apple trees in his orchard. This makes up (3)/(8) of his entire orchard. How many acres make up the farmer's entire orchard?