Question

, A 50 kg astronaut weighs 490 N. What would she way if she landed on Jupiter‘s moon Callisto what fraction is this of her weight on earth?

Answer 1

The fraction of the weight of the astronaut on Callisto to the weight on Earth is 0.126.

Step-by-step explanation:

From Newton's Law of Motion, the weight (
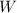`W`), measured in newtons, of an object is defined by this expression:

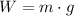`W = m\cdot g` (1)

Where:

`m` - Mass, measured in kilograms.

`g` - Gravitational acceleration, measured in meters per square second.

The gravitational acceleration in Callisto is 1.236 meters per square second.

If we know that
`m = 50\,kg` and
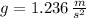`g = 1.236\,(m)/(s^(2))`, then the weight of the astronaut in Callisto is:

`W = (50\,kg)\cdot \left(1.236\,(m)/(s^(2)) \right)`

`W = 61.8\,N`

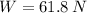
And the fraction is:

`x = (61.8\,N)/(490\,N)`

`x = 0.126`

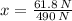
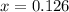
The fraction of the weight of the astronaut on Callisto to the weight on Earth is 0.126.