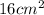The area of triangle ABC is
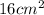
To find the area of triangle ABC, you can use the formula for the area of a triangle, which is 1/2 * base * height.
The area of triangle ABC is
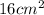
To find the area of triangle ABC, we can use the formula for the area of a triangle, which is 1/2 * base * height.
In this case, the base of the triangle is BC and the height is AM.
Since AM is perpendicular to BC and forms a right angle at M, AM is the height of the triangle.
Therefore, the area of triangle ABC is:
Area = 1/2 * BC * AM
Area = 1/2 * 8 cm * 4 cm
Area =
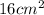
Therefore, the correct answer is B.
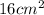
The probable question may be:
In triangle ABC, Side BC=8cm, a perpendicular line is drawn from point A to BC as AM=4cm, angle AMC=90 degree . Find the area of triangle.
A.
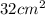
B. 16 cm
C. 32 cm
D.